Now, let's expand the ratio spread of the prior example into a 1x3, and see how the picture changes. This will set up the graphic intuition a bit further. Our position now is:

Long one 100 call,
Short three 110 calls

Where is the closing call wing strike here? Let's look at the pictures: The profit/loss payoff of this position is less well known, but still trivial. Again ignoring premia at expiration, we have:  

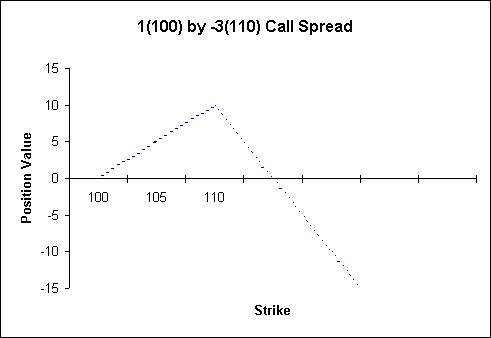
Again, the directional risk in this position begins at strike X and increases without bound with the underlying. This time you will note that the slope of the downward line is twice that of the upward line. This is because we are net two calls short, (= long one call, short 3 calls) whereas in the previous example we were one call short. This implies that to neutralise the ratio spread by creating an odd-shaped butterfly, we will need to purchase two closing calls.                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

In the previous symmetric butterfly example, the distance from the inside strike to the closing, outside strike as 20, and the distance from the short (soon to become middle) strike to the outside strike was 10, which was equal to the distance from the inside strike to the middle strike (the minus sign is the "distance" operator so this was equal to 110-100). What is the closing strike going to be here?   In this example, you might guess (or pick off the graph) that the closing strike will be set at 115, and that we need two options to negate the directional risk of the position from that point onwards:  

 

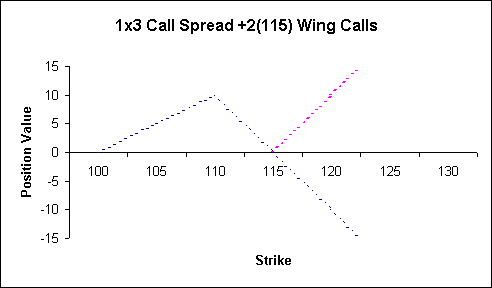
Note that the same graphic neutralisation analysis applies to this 1x3 as applied to the 1x2 in the prior example.            

 

 

 

 

 

 

 

 

 

 

 

 

The two positions sum to zero, this time above 115, leaving us with a less well known, but still traded, assymetric butterfly:    tidbit

Long 1x 100 Call

Short 3x 110 Call

Long 2x 115 Call  

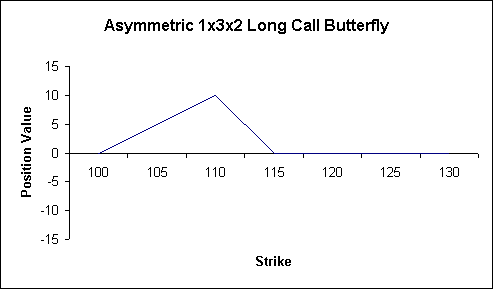
Here, again ignoring premia, we have a crack at making money anywhere between 100 and 115 and no losses that arise anywhere else.

Now, examining this poor misshapen critter, we can derive the following intuition about how many options we need to close the butterfly, and where they should be: To turn unlimited directional risk into bounded directional risk with a naked spread, we will always need to buy back the number of options that we are net short. In this case we were Short 3, Long 1 option, in other words, Net Short two options.

The furthest distance that the closing strike can be must be a function of the distance between the opening and middle strikes of the spread, stretched or scrunched by number of options Net Short. (The stretch or scrunch operator is the division sign).

In the case at hand, the distance between the middle strike of the fly and the closing strike of the fly (110 - 115) is equal to the distance between the opening and middle strikes (100 - 110), scrunched by the slope of the unbounded risk we want to neutralise (-2) which is equal to the number of calls we are net short (+1 -3). Neutralising a position will mean taking its mirror image geometrically, which is equivalent to multiplying by -1.

Expressed arithmetically, to close the 1(100) x -3(110) call spread, we need

-1*(+1-3)=2 Calls, struck at (proceeding from left to right)

3(100 - 110) / (1-3) = -30 / -2 = +15 points away from the opening strike.

So we buy 2 calls struck at 115 to complete this butterfly.

---

Now, this works where the ratio spread is less than 2:1 as well:

Assuming the following position:

Long two 100 Calls

Short three 110 Calls

The remaining wing of the asymmetric butterfly would be +1 Call struck at 130:

 

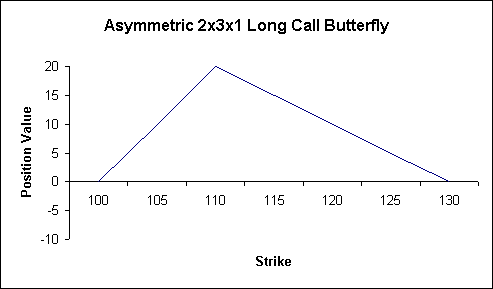
So much for the intermediate geometric insight. We'll develop these points as well, but for the moment we should emphasise and extend the practical result:

We can view any ratio spread as merely an incomplete, perhaps asymmetric, butterfly.